1 - Détermination du nombre de bits n.

Si l'on veut réaliser, à partir de bascules JK, un compteur de 0 à N, alors il faut disposer de n bascules, n étant l'entier le plus petit tel que

2 - Détermination de la table des états.

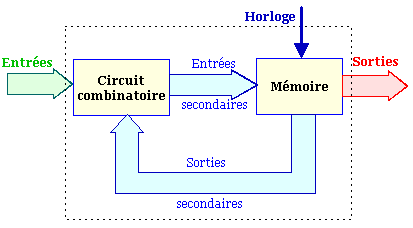
Un compteur synchrone est un circuit séquentiel dans lequel l'état présent à l'instant tk de la k ième impulsion d'horloge dépend des entrées secondaires à cet instant, elles-mêmes résultant d'une combinaison logique des entrées primaires du circuit et des sorties secondaires de la mémoire (ensemble des bascules de sortie).

L'état suivant, qui apparaîtra à la k+1 ième impulsion, dépendra donc des variables de sortie secondaires élaborées à l'instant tk.

Il est donc nécessaire de remplir une table de tous les états logiques possibles en sortie à un instant tk (même les états impossibles en théorie, mais qui pourraient apparaître à la mise sous tension ou en cas de parasites), et des états suivants à tk+1.
On choisira arbirairement dans l'exemple ci-joint de faire suivre les états impossibles par l'état de repos 0000.

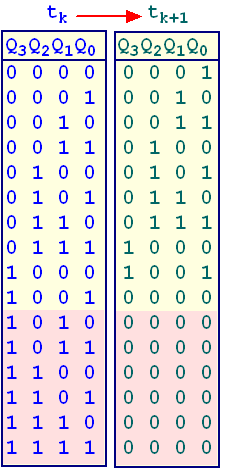
Exemple ci-contre : conception de la table des états pour un compteur décimal codé binaire.
Ce compteur, qui compte de 0 à 9, nécessite n=4 bits. La table des états contient 6 états impossibles, de 1010 (valeur décimale 10) à 1111 (valeur décimale 15).

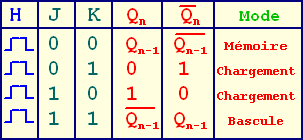
3 - Détermination de la table des entrées Ji et Ki.

On rappelle qu'au moment de l'impulsion active de l'horloge, une bascule JK prend des états en sortie dépendant des entrées J et K, selon le tableau ci-contre.

L'examen de la table des états des sorties ci-dessus, qui fournit Qi(tk) et Qi(tk+1) permet de créer une table pour chaque variable d'entrée Ji et Ki à l'instant tk+1, en fonction des valeurs des Qi(tk).

Si l'une de ces variables peut prendre un état indifférent, on la représente par la lettre X.

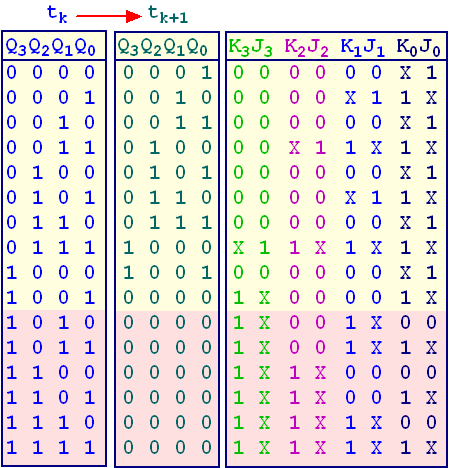
4 - Simplification des équations des Ji et Ki.

A partir de la table ci-contre on déduit, puis on simplifie par une méthode algébrique ou graphique, les équations des différentes entrées secondaires Ji et Ki, en fonction des sorties Qi à l'instant tk.

Il est conseillé pour n inférieur ou égal à 4 d'utiliser les méthodes de simplification par tableaux de Karnaugh.

On remarquera que si l'on ne tient pas compte des états impossibles, l'écriture des variables d'entrée secondaires est plus simple. En particulier, la première bascule fonctionne en flip-flop (bascule) avec J0=K0=1, J1=K1, etc.

Sinon, on vérifiera que :

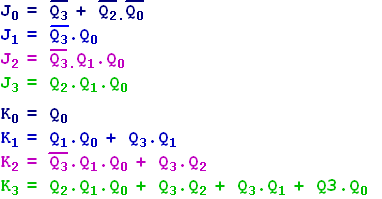
5 - Matérialisation du circuit.

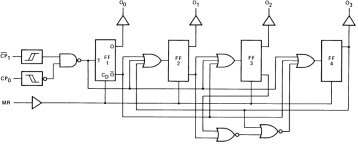
Il suffit à partir de bascules JK et de portes logiques de câbler les équations simplifiées obtenues précédemment.

C'est en utilisant une méthode de ce type que l'on arrive à la matérialisation du circuit MSI HEF4518 ci-contre.

Cette méthode conduit à des circuits de report parallèle. Leur avantage est de ne pas cumuler les temps de propagation des informations au travers des portes logiques utilisées pour le codage de Ji et des Ki, comme dans le cas du report en série.

Mais on constate que le câblage des entrées secondaires est de plus en plus complexe au fur et à mesure que le poids binaire des fonctions augmente.